[Machine Learning] 선형 모델(Linear model) 을 이용한 예측 모델 만들기
*K-최근접 이웃 알고리즘을 이용한 모델은 예측이 느리고 많은 특성을 처리하는 능력이 부족하다. 이러한 단점이 없는 모델이 바로 선형 모델(Linear model)이다.
선형 모델(Linear model) : 각 특성에 해당하는 기울기들을 곱한 후(특성 1개당 기울기 1개를 가지게 됨) 이를 모두 더하여 예측에 사용하게 된다. 특성이 하나일 경우 직선, 두 개일 경우에는 평면, 그 이상의 평우 초 평면 형태가 된다.
1. 선형 회귀(Linear Regression, 최소제곱법) : 예측과 훈련 세트에 있는 타깃 y 사이의 평균제곱오차를 최소화하는 파라미터 w, b를 찾는 알고리즘. (평균 제곱오차 : (예측값-타깃값)^2 / 샘플의 개수 )
1) 데이터 셋이 단순하여 과소적합인 상태


2) 데이터 셋이 복잡하여 과대적합인 상태


2. 리지 회귀(Ridge Regression) : 기본 선형 회귀 방식에서 나타날 수 있는 과대적합 문제를 해결하며 복잡도를 제어할 수 있는 알고리즘으로서, 가중치를 최대한 작게 만들어 모든 특성이 출력에 주는 영향을 최소한으로 만드는 모델
- alpha 매개변수를 통하여 모델의 훈련, 테스트 세트 점수 조절 가능(alpha의 값이 0에 가까울 수록 훈련 세트의 성능은 낮아지지만, 테스트 세트의 성능은 높아짐)

3. 라소 회귀(Lasso Regression) : Ridge에 대한 대안으로서, 계수를 0에 가깝게 만들려고 하는 모델이다. 리지 모델이 더 선호되곤 하지만, 특성이 많고 그 중 일부분만 중요하다면 라소 회귀가 더 선호된다.

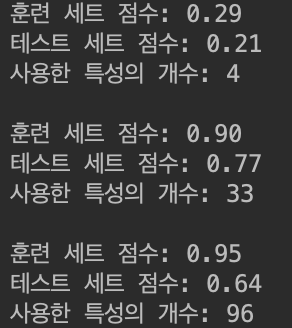
alpha 값을 줄이는 만큼 계수에 대한 제약이 풀리므로 규제의 효과가 없어져, 과대적합이 되어 LinearRegression으로 만들어진 모델과 비슷해진다.